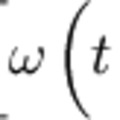Keresés

Poseidon 2010.03.25. 12:43

Nyúton törvénye Vol.2

Egy pontszerű test 'a' gyorsulása egyenesen arányos a testre ható, a gyorsulással azonos irányú 'F' erővel, és fordítottan arányos a test 'm' tömegével.

A törvény képlettel kifejezett, elterjedt formája: F = ma, ahol

  • F az erő vektora
  • m a gyorsítandó tömeg
  • a a gyorsulás vektora

Az összefüggés megmutatja, hogy minél nagyobb egy testre ható erők eredője, annál nagyobb a test gyorsulása. A törvény definiálja tömeg fogalmát, amely a testek állandó jellemzője, az erő és a gyorsulás arányának meghatározója.

A törvény általánosabb formáját akkor kapjuk, ha az erőt az I impulzusvektor időegységre eső megváltozásaként definiáljuk (I = mv, ahol v a sebesség vektora):

\mathbf{F}=\frac{d\mathbf{I}}{dt}

Általános esetben mind a sebesség, mind a tömeg időtől függő mennyiség, tehát

\mathbf{F}=\frac{d\mathbf{I}}{dt} = \frac{d}{dt}(m\mathbf{v}) = m\frac{d\mathbf{v}}{dt} + \mathbf{v}\frac{dm}{dt} = m\mathbf{a} + \mathbf{v}\frac{dm}{dt}

Az F = ma alakkal ellentétben ez az összefüggés akkor is érvényes, ha a tömeg idővel változik (például egy rakéta esetében). Az egyszerűbb alakot kapjuk, ha feltételezzük, hogy a tömeg állandó, így a dm/dt tag nullával helyettesíthető.

 

Facebook Tumblr Tweet Pinterest Tetszik
0

Szólj hozzá!

Címkék: törvény newton nyúton

Ajánlott bejegyzések:

Kommentek:

A hozzászólások a vonatkozó jogszabályok  értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai  üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a  Felhasználási feltételekben és az adatvédelmi tájékoztatóban.

Nincsenek hozzászólások.
süti beállítások módosítása